Chapter 3
Diodes
The most fundamental nonlinear element of electronic circuits is the semiconductor junction diode. Because of its importance in both discrete and integrated circuits, the creators of Spice have made provisions for a built-in model of the semiconductor diode. In this chapter we shall outline how to access the diode model, and how to alter the model parameters to suit particular applications. Finally, using Spice, we shall investigate the behavior of some commonly used diode circuits, and compare the results with those obtained through the approximate hand analysis methods presented in the text by Sedra and Smith, 3rd Edition.
3.1 Describing Diodes to Spice
A pn junction diode is described to Spice using two statements. One statement is necessary to specify the diode type and the manner in which it is connected to the rest of the network, and the other statement is required to specify the values of the parameters of the built-in model for the diode type specified by the first statement. In the following we shall describe these two statements.
3.1.1 Diode Element Description
The presence of a pn junction diode in a circuit is described to Spice through the Spice input file using an element statement beginning with the letter D. If more than one diode exists in a circuit, then a unique name must be attached to D to uniquely identify each diode. This is then followed by the two nodes that the anode and cathode of the diode are connected to. Subsequently, on the same line, the name of the model that will be used to characterize this particular diode is given. The name of this model must correspond to the name given on a model statement containing the values of the model parameters. Lastly, one has the option of specifying the number of diodes that are considered to be connected in parallel. This acts as a convenient way of scaling the cross-sectional area of the device.
For quick reference, we depict in Fig. 3.1 the syntax of the Spice statements pertaining to the pn junction diode. We shall discuss the model statement more fully next.

Fig. 3.1: Spice element description for the pn junction diode. Also listed is the general form of the associated diode model statement. A partial listing of the parameter values applicable to the pn junction diode is given in Table 3.1.
3.1.2 Diode Model Description
As is evident from Fig. 3.1, the model statement for the pn junction begins with the keyword .MODEL and is followed by the name of the model used by a diode element statement, the letter D to indicate that it is a diode model, and a list of the values of the model parameters (enclosed between brackets). There are quite a few parameters associated with the pn junction diode model used by Spice, and their individual meanings are rather involved. Instead of trying to describe the meaning of every parameter, we shall only consider here the parameters of the Spice diode model that are relevant to our introductory study of diodes in this chapter.
|
Fig. 3.2: The Spice large-signal pn junction diode model.
|
Fig. 3.3: A small-signal equivalent circuit used by Spice to represent a semiconductor diode.
|
The large-signal model used for the semiconductor junction diode in Spice is shown in Fig. 3.2. The DC characteristic of the diode is modeled by the nonlinear current source iD which depends on vD according to the following equation:
(3.1)

Here IS, n and VT are device parameters: IS is referred to as the saturation current, n the emission coefficient, and VT as the thermal voltage. Both IS and n are related to the physical make-up of the diode, in contrast to the thermal voltage VT which depends on the temperature of the device and two physical constants, i.e.,
(3.2)

Here k is Boltzmann's constant (k=1.381 x 10-23 V C/°K), T is the absolute temperature in degrees Kelvin, and q is the charge of an electron (q=1.602 x 10-19). In many approximate analyses, VT is assumed to equal 25 mV at a room temperature of 290 °K. However, Spice does not approximate this quantity, and instead uses the exact values of k, T and q to determine VT.
Finally, the series resistance rS in the diode model shown in Fig. 3.2 simply models the lump resistance of the silicon on both sides of the semiconductor junction. The value of rS may range from 10 to 100 W in low-power diodes.
Under small-signal conditions, Spice adopts the diode equivalent circuit shown in Fig. 3.3. Here rd is the incremental resistance of the diode around its quiescent operating point and is expressed in terms of the DC bias current ID as follows:
(3.3)

Spice does not use the name rd for the small-signal resistance of the diode, instead it refers to this resistance in the Spice output file as REQ.
Under large reverse-bias conditions (i.e., vD << 0), the operation of the semiconductor diode is dominated by physical effects other than those which give rise to Eqn. (3.1). More specifically, under large reverse-bias conditions, the semiconductor diode enters its breakdown region and begins to conduct a large reverse current. In Spice, the dependence of this reverse current on reverse voltage is modeled as an exponential function - much like that of the forward bias region. In fact, for voltages below a commonly specified reverse-bias voltage -VZK (breakdown voltage) the i-v characteristic is a near vertical straight line. Correspondingly, at this breakdown voltage -VZK, the diode is said to conduct a reverse current of -IZK. Thus, VZK and IZK specify the start of the breakdown region of the semiconductor diode. Note that these two quantities are positive numbers.

Table 3.1: A partial listing of the Spice parameters for a static pn junction diode model.
A partial listing of the parameters associated with the Spice pn junction diode model under static conditions is given in Table 3.1. The first column lists the symbol used to denote each parameter as described in this chapter. For the most part, the symbol of each of these parameters corresponds with those used in Chapter 3 of Sedra and Smith. The next column lists the corresponding name of the parameter used by Spice; this is the only name that can be used for this parameter in the list of model parameters on a .MODEL statement. Also listed are the associated default values which the parameter assumes if a particular value is not specified on the .MODEL statement. To specify a parameter value one simply writes, for example, Is=1e-13, n=2, BV=50, IBV=1e-12, etc.
3.2 Spice as a Curve Tracer
Whenever a model of a device is created, whether it be a model of an op-amp, diode or some other electronic device, one should make certain the expected terminal characteristics are actually captured by the model. In the laboratory, a curve tracer is an instrument that is commonly used to measure the DC terminal characteristics of semiconductor devices. Using Spice, we can emulate the behavior of the curve-tracer and therefore determine whether the DC model chosen to represent the diode is suitable.
A curve-tracer is an instrument designed to measure the i-v characteristics of semiconductor devices over a wide range of voltage and current levels. A typical curve-tracer instrument contains a set of variable voltage and current sources that are capable of varying their level beginning at some lower value and proceeding to some maximum value in discrete steps. Concurrently, the current supplied to - or the voltage that develops across - the externally attached device is measured and recorded. On completion, the results are displayed on the screen of a cathode ray tube (CRT) as a graph. To emulate this behavior using Spice we make use of the DC sweep command in conjunction with some DC source.
For example, in Fig. 3.4 we display a voltage source (VD) with a single diode Dtest as its load. We shall assume that the diode is a ``1 mA diode’’ (meaning that it conducts a current of 1 mA at a forward bias voltage of 0.7 V) and that its voltage drop changes by 0.1 V for every decade change in current. Thus, using the diode current equation listed in Eqn. (3.1), one can show that this diode is characterized by IS=100 pA and n=1.679. To describe this particular 1 mA diode to Spice, we use the following model statement:
.model 1mA_diode D ( Is=100pA n=1.679 ).
Now, to compute and display the forward-bias i-v characteristics of this 1 mA diode we shall sweep VD in Fig. 3.4 from 0 V to 800 mV in 10 mV steps using the following DC sweep command
.DC VD 0V 800mV 10mV
and then plot the diode current as a function of this voltage. Although the diode current is not directly accessible by Spice[1] it is equal to the current supplied by the voltage source VD which is readily accessible by Spice. We shall therefore plot the current supplied by VD. Recall that according to Spice conventions, the current supplied by a voltage source is negative, thus the current plotted by Spice will be opposite to that which flows through the diode. Fortunately, the plot routine of Probe enables one to plot -I(VD).
The Spice input deck for this particular example is listed in Fig. 3.5 and the resulting i-v characteristic for this particular diode is shown in Fig. 3.6 in two different forms. The top curve displays the diode i-v characteristic on a linear scale, whereas the bottom curve is on a semi-logarithmic scale.
The reverse-bias characteristics of a particular diode are computed in exactly the same manner as that used to compute the forward-bias diode characteristics. In fact, one can combine both the forward- and reverse-bias characteristics onto one i-v plot. Consider comparing the forward- and reverse-bias characteristics of the 1 mA diode used above (the breakdown region of which was not specified, i.e., left for Spice to use default values) to a similar one that has a breakdown region defined by VZK=10 V and IZK=1 nA. The Spice model statement for this new diode would be as follows:
.model bkdwn_diode D (Is=100pA n=1.679 BV=10V IBV=1nA).
The resulting i-v characteristics for these two diodes are displayed in Fig. 3.7. Clearly, both these diodes have identical forward-bias characteristics but very different reverse-bias behavior.
|
Fig. 3.4: Simple circuit arrangement for determining the i-v characteristic of a 1 mA diode.
|
Spice As A Curve Tracer: Diode I-V Characteristics
** Circuit Description ** VD 1 0 DC 700mV Dtest 1 0 1mA_diode * diode model statement .model 1mA_diode D (Is=100pA n=1.679) ** Analysis Requests ** * vary diode voltage and measure diode anode current .DC VD 0V 800mV 10mV ** Output Requests ** .plot DC I(VD) .probe .end
Fig. 3.5: Spice input deck for determining diode forward-bias characteristics.
|
|
Fig. 3.6: Forward-bias characteristics of a 1 mA diode with an emission coefficient of 1.679; upper curve: linear scale, lower curve: semilogarithmic.
|
Fig. 3.7: Comparing the i-v characteristic of a 1 mA diode with a breakdown region specified by VZK=10 V and IZK=1 nA, and one that has no breakdown region specified.
|

Table 3.2: The general syntax of the Spice command for setting the temperature of a circuit.
3.2.1 Extracting the Small-Signal Diode Parameters
If an operating point (.OP) analysis command is included within the Spice input file, then the small-signal parameters of each diode within the circuit described to Spice will be evaluated by Spice and listed in the output file. For example, the small-signal parameters of the 1 mA diode used in the above example biased at 700 mV, would be found in the Spice output file as follows:
|
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C
**** DIODES
NAME Dtest MODEL 1mA_diode ID 1.00E-03 VD 7.00E-01 REQ 4.34E+01 CAP 0.00E+00
|
Included in this list of operating point information is the name of the diode assigned by the user and the name of the model used to characterize the diode. This is followed by the DC bias point information, ID and VD, and then, the incremental resistance of the diode REQ. At the bottom of this list is the small-signal capacitance CAP associated with this diode. We shall defer discussion of this parameter until Chapter 7.
At this point it would be highly instructive to check that the small-signal resistance of the diode computed by Spice in the list of operating point information agrees with that computed by the simple formula rd = nVT/ID. Consider, for this particular diode, n=1.679, VT=25.8 mV and ID=1 mA. Thus, on substituting these values into the expression for rd, we get 43.47 ohm, almost in perfect agreement with the value computed by Spice (43.4 ohm).
One will notice in the above list of operating point information that the temperature at which the analysis has been performed is also indicated. In this case, the operating point analysis was performed at a room temperature of 27 °C. The temperature at which the circuit is simulated by Spice can be changed by the user. The next example will demonstrate how this is accomplished.
3.2.2 Temperature Effects
To investigate the effect of temperature variation on diode behavior we simply repeat the above curve-tracer analysis at different temperatures. To accomplish this, one just adds a .TEMP statement with the temperature (in degrees Celsius) at which the analysis should be performed. If more than one temperature is listed, then the analysis will be repeated for each temperature. A general description of the syntax of this command is provided in Table 3.2. For the example above, let us compute the diode i-v characteristics for temperatures of 0°, 27° and 125°C. The statement that should be added to the Spice deck shown in Fig. 3.5 is:
.TEMP 0 27 125.
The Spice job is then re-run and the results are shown in Fig. 3.8. The results displayed in this graph were restricted to lie within a 0 to 1 mA current range by adjusting the scale of the y-axis. This was deemed necessary in order to best illustrate the diode characteristics for all three temperatures on one graph. It should be evident form Fig. 3.8 that as the temperature increases the i-v curve for the diode shifts to the left. Close scrutiny using the cursor facility of Probe (found in PSpice) reveals that for a constant current of 0.4 mA the forward diode voltage decreases by about 1.7 mV for every degree C increase in temperature.
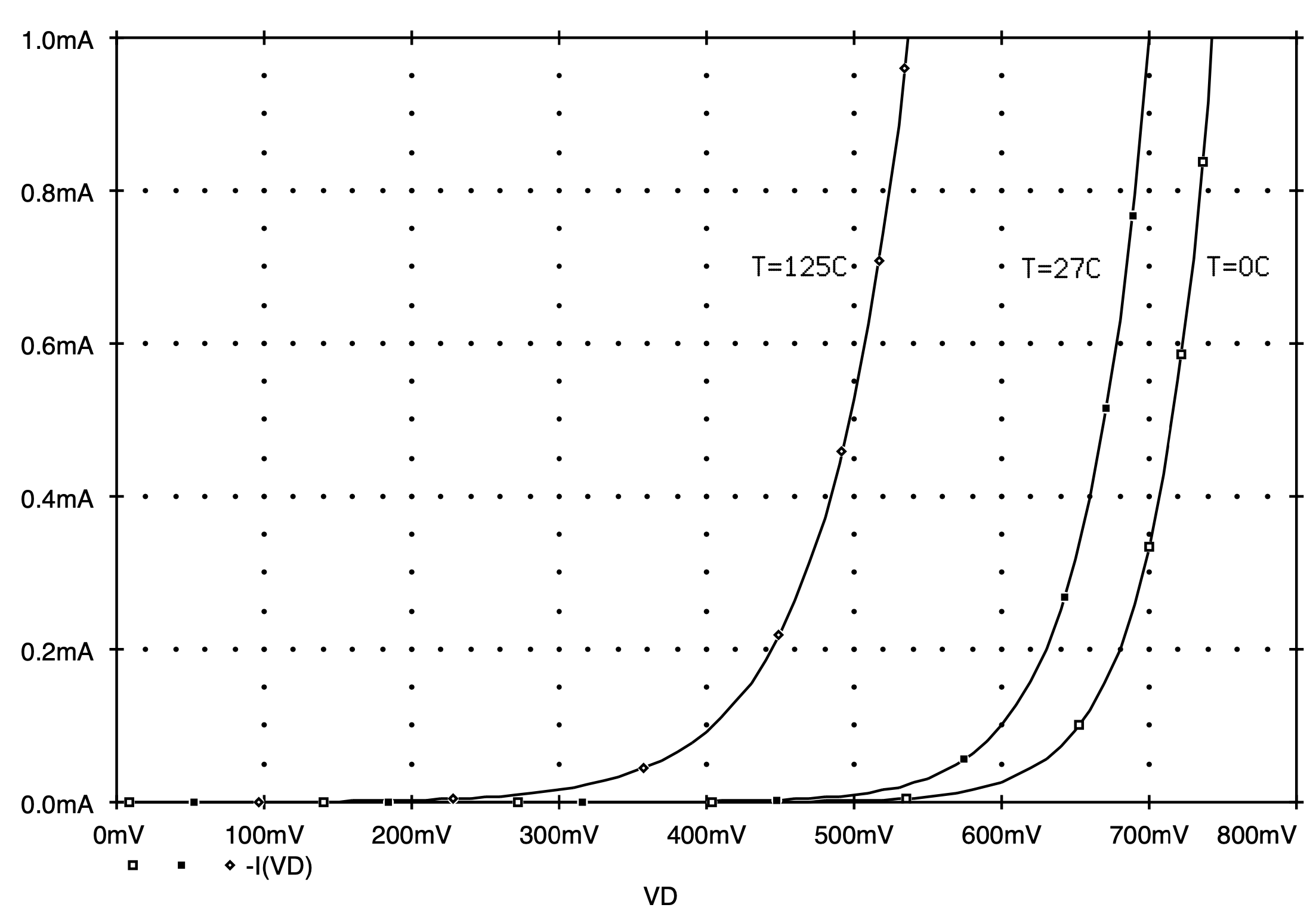
Fig. 3.8: Illustrating the temperature dependence of the forward bias characteristics of a 1 mA diode.
3.3 Approximating Ideal Diode Behavior
The ideal diode concept often simplifies the analysis of electronic circuits containing diodes by assuming that the forward bias voltage across a conducting diode is zero regardless of the level of current flowing through it, and conversely, when in the blocking state, it prevents current from flowing through it regardless of the level of reverse bias voltage appearing across it. An ideal model for a diode does not exist in Spice for the simple reason that an ideal diode does not exist in practise. However, there are numerous occasions when an ideal diode is useful to have; especially when attempting to represent an arbitrary nonlinear function.
Consider the equation for the static diode current given in Eqn. (3.1) and repeated below for convenience,

There are two parameters associated with this equation that are under our direct control: the saturation current IS and the emission coefficient n. Our problem is to adjust one, or both, of these parameters, such that (a) vD tends towards zero when the diode is considered on, and (b) iD tends towards zero when it is considered off. On examination of Eqn. (3.1) we see that condition (b) is satisfied when IS is reduced and/or n is increased (recall that vD is negative). Conversely, from the equation depicting the diode voltage (a simple re-arrangement of Eqn. (3.1)),
(3.4)

we see that alterations will tend to increase vD under forward bias condition instead of reducing it. This suggests that conditions (a) and (b) cannot both be met simultaneously by adjusting either IS or n. We notice from Eqn. (3.1), however, that under reverse bias conditions that regardless of the value of n, iD will never exceed IS - a near-zero value. Thus, a good approximation to ideal diode behavior is obtained by making n small because this will reduce the diode forward voltage drop and maintain low reverse-bias current. Experience has shown that a value for n between 0.01 and 0.001 works well. Values smaller than 0.001 usually result in DC convergence problems. Fig. 3.9 illustrates the i-v characteristics of a simple diode characterized by the following model statement:
.model ideal_diode D (Is=100pA n=0.01).
For all intents and purposes, the curve shown in Fig. 3.9 is an excellent representation of ideal diode behavior.

Fig. 3.9: i - v characteristics of a near-ideal diode.
3.4 Voltage Regulation Using a String of Diodes
Connecting one or more diodes in series with a resistor and a power supply provides a simple means of creating a relatively constant voltage, somewhat independent of fluctuations in the power supply level. One example of this is demonstrated in Fig. 3.10(a) where three diodes and a 1 k-ohm resistor are connected in series with a +10 V DC voltage source. Since the forward voltage drop of each diode remains almost constant at approximately +0.7 V for a wide range of diode currents, the voltage that appears at the output of this regulator circuit is about +2.1 V. With the aid of Spice, we would like to investigate the effect of the fluctuations in the +10 V supply on the output voltage. We shall assume that the fluctuations are caused by a 60 Hz, 1 V-peak sinusoidal signal riding on the +10 V DC voltage level. This arrangement is illustrated in part (b) of Fig. 3.10. This same example was analyzed by hand in Example 3.7 of Sedra and Smith, 3rd Edition. Once the Spice results are obtained, we shall compare them with those obtained by hand.
|
Fig. 3.10: (a) A 2.1 V voltage regulator circuit consisting of three diodes in series. (b) Representing the power supply fluctuation with a 60 Hz, 1 V-peak sinusoidal signal superimposed on a constant DC voltage of +10 V.
|
A Three Diode String Voltage Regulator Circuit
** Circuit Description ** * DC supply + AC ripple Vs 3 0 DC +10V Vripple 1 3 sin (0 1V 60Hz) * diode circuit R 1 2 1k D1 2 4 diode D2 4 5 diode D3 5 0 diode * diode model statement .model diode D (Is=831.5pA n=2) ** Analysis Requests ** .OP .TRAN 0.5ms 100ms 0ms 0.5ms ** Output Requests ** .PLOT TRAN V(2) .PROBE .end
Fig. 3.11: The Spice input file for computing the time-varying output voltage of the voltage regulator circuit shown in Fig. 3.10. |
In Fig. 3.11 we list the Spice input file for this circuit. The three diodes are assumed to have model parameters: IS=831.5 pA and n=2. A transient analysis is requested to compute the behavior of this regulator circuit over six periods of the 60 Hz input signal. On average, 33.3 points-per-period of the input signal (i.e., a sampling interval of 0.5 ms) are to be collected. This will provide enough points so that a smooth graph of the output waveform can be plotted. Also included in this Spice deck is a request for an operating point (.OP) analysis.
Before we submit this input file to Spice for processing, we shall concatenate on the end of it another Spice deck. This Spice deck will be identical to that seen in Fig. 3.11 except that the output of the voltage regulator circuit is loaded with a 1 k-ohm resistor. The element statement required to be added to the Spice deck would be as follows:
Rload 2 0 1k.
On completion of the two Spice jobs, we plot the output waveforms from the voltage regulator circuit in Fig. 3.12. The bottom curve is the output voltage waveform of the regulator circuit having a 1 kW load, and the curve above it is the output voltage signal of the regulator circuit under no-load conditions. As is evident, the output voltage waveform from the unloaded regulator circuit is sinusoidal, having the same frequency as the power supply fluctuations (60 Hz). It has an average value of 2.486 V, slightly different from that estimated above (2.1 V) assuming the voltage drop of each diode is 0.7 V. The peak-to-peak excursion of this output voltage signal is found using the cursor facility of Probe to be 40.7 mV. This is obviously much less than the peak-to-peak excursions of the power supply fluctuations of 2 V. In the case of the loaded regulated circuit, we see that the output voltage signal is riding on a DC level of 2.426 V, a decrease in the DC level of 60 mV below that of the unloaded regulator circuit. The peak-to-peak amplitude of the ripple superimposed on the output voltage is found to have increased to 57.4 mV.

Fig. 3.12: The output voltage signals from the three-diode string voltage regulator shown in Fig. 3.10 assuming that the power supply voltage varies sinusoidally with an amplitude of 1 V. The bottom waveform is the output of the regulator with a 1 kW load and the one above it is with no load.
According to small-signal analysis (see Example 3.7 of Sedra and Smith), the expected output voltage ripple of the unloaded diode regulator circuit subject to power supply fluctuations vac is simply given by the following expression:
(3.5)
![]()
where rd is the incremental resistance of each diode. The incremental resistance of each diode as calculated by Spice is found in the Spice output file amongst the DC operating point information. For the unloaded regulator case, these are shown below:
|
**** DIODES
NAME D1 D2 D3 MODEL diode diode diode ID 7.51E-03 7.51E-03 7.51E-03 VD 8.29E-01 8.29E-01 8.29E-01 REQ 6.88E+00 6.88E+00 6.88E+00 |
As is evident, each diode has an incremental resistance (rd) of 6.88 ohm. Interestingly enough, this is quite close to the value predicted by simple hand analysis at 6.3 ohm; a result obtained by assuming a 0.7 volt-drop across each diode leading to a diode current of 7.9 mA. Substituting, rd=6.88 ohm into Eqn. (3.5) above, and assuming a 2 V peak-to-peak input signal, results in an estimated output peak-to-peak voltage signal of 40.4 mV: very close to the value of 40.7 mV found by Spice.
In the case of the 1 k-ohm loaded regulator circuit, hand analysis also leads to a similar confirmation. Small-signal analysis of the three-diode regulator circuit with a 1 k-ohm load leads to an output voltage given by the expression:
(3.6)
![]()
Substituting the appropriate circuit parameters, together with the incremental resistance of each diode as calculated by Spice, and shown below,
|
**** DIODES
NAME D1 D2 D3 MODEL diode diode diode ID 5.15E-03 5.15E-03 5.15E-03 VD 8.09E-01 8.09E-01 8.09E-01 REQ 1.01E+01 1.01E+01 1.01E+01
|
we find
![]()
It is interesting to note that the addition of the load resistance has acted to increase the incremental resistance of each diode. This is a result of the 1 k-ohm load drawing a current away from the diode string (the diode current has been reduced by 2.36 mA). For a 2 V peak-to-peak power supply variation, the expected time-varying output voltage signal is then 57.1 mV, in close agreement to the value of 57.4 mV calculated by Spice.
3.5 Zener Diode Modeling
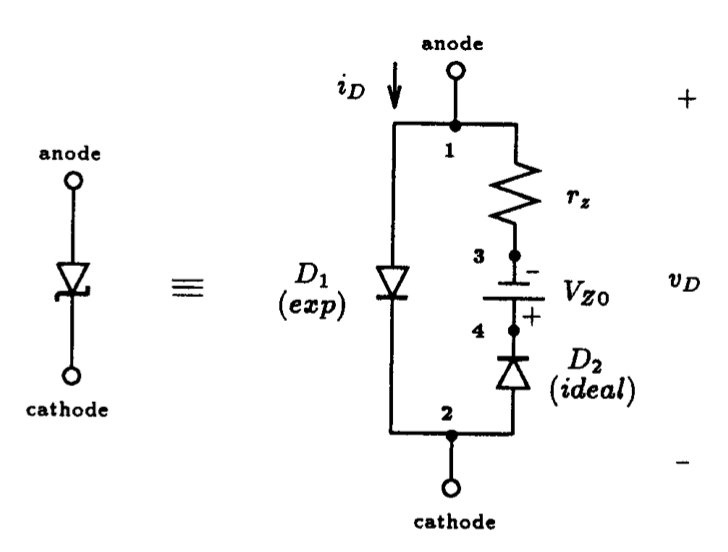
Although the start of the diode breakdown region defined by VZK and IZK can be specified on a diode model statement using the Spice parameters BV and IBV, no control is provided for the user to specify the characteristics of the breakdown region, i.e., slope of the i-v curve in the breakdown region[2]. It is common for zener diode manufacturers to specify the shape of the breakdown region by specifying the inverse of the slope of the almost-linear i-v curve at some operating point (VZ, IZ) inside the breakdown region. This inverse-slope parameter has dimensions of resistance and is known as the dynamic resistance of the zener, denoted as rz.
To model a zener diode the equivalent circuit shown in Fig. 3.13 is sometimes used. When vD > -VZ0, ideal diode D2 is consider cut-off and the terminal characteristics of the zener diode are determined solely by diode D1. Conversely, when vD > -VZ0, ideal diode D2 turns on, whereby a voltage of vD + VZ0 appears across resistor rz. The resulting current that flows through this resistance will be much greater than the reverse-bias leakage current that flows through diode D1, and therefore, the current that dominates the breakdown region of the zener diode is given by the following equation,
(3.7)

The value of VZ0 is not specified directly by the zener diode manufacturer but can be derived from the operating point information at which the dynamic resistance is obtained. It is found from the expression
(3.8)
![]()
The following example will illustrate a common application of a zener diode.
|
Fig. 3.13: A circuit model of a Zener diode. |
Fig. 3.14: A simple voltage regulator circuit with load using a single zener diode.
|
Voltage Regulation using a Zener Diode
Rather than using a string of diodes to create a simple voltage regulator circuit, a single zener diode can be used in its place, as shown in Fig. 3.14. In Example 3.9 of Sedra and Smith, one such regulator circuit was designed for an output voltage of approximately 7.5 V, assuming that the raw supply voltage fluctuates between 15 and 25 V and that the load current can vary between 0 and 15 mA. The zener diode available has a voltage drop of VZ=7.5 V at a current of 20 mA, and its rz equals 10 ohm. The current limiting resistor R in series with the zener diode was chosen at 383 ohm so that the minimum current through the diode never drops below 5 mA. Based on this design, both the line and load regulation were found to be 25.4 mV/V and -9.7 mV/mA, respectively. Using Spice, together with the model described above for the zener diode, we would like to confirm that the design requirements are indeed met. Further, we would like to check the line and load regulation directly from simulation results.
To carry out this investigation, we use the circuit setup shown in Fig. 3.15. Here the raw power supply level is modeled with two sources: a DC voltage source VS to model the average value of the power supply level, and a time-varying voltage source vripple to model the fluctuations of the power supply. Specifically, the level of the DC source is set at 20 V, and the fluctuations are modeled as a sinusoidal signal having a peak amplitude of 5 V. The frequency of this source is arbitrarily selected to be 60 Hz. To mimic possible load current fluctuations, a single current source is connected across the output terminals of the voltage regulator. We shall begin our first simulation with the value of this current source set to zero in order to first determine the behavior of the regulator under no-load conditions. A zero-valued voltage source is connected in series with the zener diode to monitor the current through it, and another is also placed in series with the current source iLoad for the same reason.
The model for the zener diode is the equivalent circuit shown in Fig. 3.13. The value of rz is simply that specified in the problem at 10 ohm. The value of VZ0 is determined from Eqn. (3.8) and the data supplied for the zener diode (given above), from which we find VZ0= 7.3 V. Diode D1 will be modeled as a 1 mA diode with an emission coefficient of 1.679. The ideal diode, D2, will be model with IS=100 pA and n=0.01. The subcircuit describing this particular zener diode would then appear as follows:
|
.subckt zener_diode 1 2 * connections: | | * anode | * cathode Dforward 1 2 1mA_diode Dreverse 2 4 ideal_diode Vz0 4 3 DC 7.3V Rz 1 3 10 * diode model statement .model 1mA_diode D (Is=100pA n=1.679 ) .model ideal_diode D (Is=100pA n=0.01 ) .ends zener_diode
|
The complete Spice input file describing the circuit shown in Fig. 3.15 is listed in Fig. 3.16. A transient analysis is requested so that 6 periods of the output voltage signal can be observed. The results of the Spice analysis are shown in Fig. 3.17. Both the power supply voltage VS + vripple and the voltage across the zener diode are shown. The top graph displays the supply voltage and the bottom graph displays the corresponding zener diode voltage waveform. As expected, the voltage fluctuation of the power supply is sinusoidal having a peak-to-peak amplitude of 10 V riding on a DC level of 20 V. The output voltage from the regulator circuit is also sinusoidal having a peak-to-peak amplitude of 254.7 mV and riding on a DC level of 7.628 V. The precise value of these two levels were determined using the cursor facility of Probe. One can also notice that both the input and the output voltage waveforms are in phase. Thus, we can conclude that a line voltage change of +10 V gives rise to an output voltage change of +254.7 mV. Thus, the line regulation, given by

is calculated to be +25.47 mV/V. This seems to agree almost exactly with the value determine by the simple expression for line regulation given by rz/(rz+R) derived in Chapter 3 of Sedra and Smith (i.e., 25.4 mV/V). This should not be too surprising here given that the circuit has been operating entirely in its linear region.
|
Fig. 3.15: Circuit setup used to investigate the line and load regulation of the simple zener diode voltage regulator circuit of Fig. 3.14. A zero-valued voltage source is placed in series with each of the zener diode and the current source iLoad to monitor their respective currents. They play no part in the circuit operation.
|
Zener Diode Voltage Regulator Circuit (No Load)
* zener diode subcircuit .subckt zener_diode 1 2 * connections: | | * anode | * cathode Dforward 1 2 1mA_diode Dreverse 2 4 ideal_diode Vz0 4 3 DC 7.3V Rz 1 3 10 * diode model statement .model 1mA_diode D (Is=100pA n=1.679 ) .model ideal_diode D (Is=100pA n=0.01 ) .ends zener_diode
** Main Circuit ** * power supply Vs 3 0 DC +20V Vripple 1 3 sin ( 0V 5V 60Hz ) * zener diode voltage regulator circuit R 1 2 383 XD1 4 2 zener_diode Vzener 4 0 0 * simulated load condition Iload 2 5 0A Vload 5 0 0 ** Analysis Requests ** .OP .TRAN 0.5ms 100ms 0ms 0.5ms ** Output Requests ** .PLOT TRAN V(1) V(2) .PROBE .end
Fig. 3.16: The Spice input file for computing the time-varying no-load output voltage of the zener diode voltage regulator circuit shown in Fig. 3.15.
|

Fig. 3.17: Several waveforms associated with the zener diode regulator circuit of Fig. 3.14 under no-load conditions. The top graph displays the voltage generated by the power supply and the bottom graph displays the corresponding output voltage from the regulator circuit.
|
Fig. 3.18: The output voltage of the zener diode regulator circuit of Fig. 3.14 when the load current varies between 0 and 15 mA. The top graph displays the current drawn by the load, and the bottom graph displays the corresponding output voltage from the regulator circuit.
|
Fig. 3.19: Observing a worst-case situation: The top-most graph displays the minimum power supply voltage, the middle graph displays the time-varying load current, and the bottom graph displays the current flowing through the zener diode.
|
We can perform a similar analysis to that above, but this time, with the load current varying between 0 and 15 mA. In this way we can determine the load regulation by observing the output voltage waveform. The power supply voltage will be assumed constant at +20 V. We shall assume that the load current is triangular with a minimum value of 0 mA and a maximum value of 15 mA. The frequency of this signal will be made arbitrarily equal to 30 Hz, corresponding to a period of 33.33 ms. This signal will correctly model the minimum and maximum fluctuations of the load current. Consider revising the statement for the output current source iLoad seen in the Spice deck of Fig. 3.16 according to the following:
Iload 2 5 PULSE ( 0mA 15mA 0 16.66ms 16.66ms 1us 33.33ms).
Here a triangular waveform is emulated using the source PULSE statement. The rise time and fall time are set equal to one-half the period of the triangular waveform of 33.33 ms. The pulse width is assigned a very small value of 1 us because Spice will not accept a zero value for the pulse width.
The amplitude of the ripple voltage superimposed on the DC supply voltage should be set to 0 V in order to eliminate its presence during this analysis. Therefore, the revised Spice statement for this source is changed to the following:
Vripple 1 3 sin ( 0V 0V 60Hz ).
Submitting the revised Spice job for processing, results in the output voltage waveform VO for the regulator circuit shown in the bottom graph of Fig. 3.18. The waveform shown in the top graph depicts the load current iLoad. Here the load current is triangular, as it should be, with a 15-mA peak-to-peak amplitude. The corresponding output voltage signal is also triangular of the same frequency. The peak-to-peak amplitude of this signal was found using the cursor facility of Probe to be 146.33 mV. For an average load current of 7.5 mA, the output voltage corresponds to 7.555 V. It is important to notice that the phase of the output voltage waveform is opposite to that of the load current. This suggests that for a change in the load current of +15 mA, the output voltage changes by -146.33 mV, thus suggesting that the load regulation, expressed as

would be -146.33 mV / 15 mA, or -9.7 mV/mA. This agrees exactly with the value determine by the simple expression for load regulation given by -rz||R derived in Chapter 3 of Sedra and Smith, 3rd Edition.
As a final check on this design, let us investigate the minimum current that flows through the zener diode. Observe that the zener diode current is minimum when the power supply voltage is at its minimum and the load current is at its maximum. In keeping with our earlier approach, we shall maintain the load current as a triangular wave varying linearly between 0 and 15 mA. The ripple voltage vripple simulating fluctuations in the power supply voltage will be set to a constant -5 V level. This requires that the Spice statement for this source be changed to the following:
Vripple 1 3 DC -5V.
Re-running the Spice job with the revised source statement results in the three waveforms shown in Fig. 3.19. The top graph displays the constant +15 V level associated with the power supply and the graph below it displays the load current waveform. The lowest-most graph displays the current waveform associated with the zener diode. As is evident, the current through this diode varies between 5 mA and 20 mA.
For all practical purposes, based on the Spice results above, we can conclude that all aspects of the design did indeed meet the required conditions.
|
Fig. 3.20: Half-wave rectifier circuit using a transformer with a 14:1 turns ratio to step down the line voltage of 120 V-rms to 12 V-peak.
|
Fig. 3.21: The general syntax of the Spice statements used to describe a (nonideal) transformer. The transformer turns ratio NP:NS is determined by the appropriate selection of primary and secondary inductor values, LP and LS, respectively.
|
3.4 Rectifier Circuits
One of the most important applications of semiconductor diodes is in the design of rectifier circuits. In the following, with the aid of Spice, we shall investigate two common types of rectifier circuits: the half-wave and the full-wave rectifier. In the case of the full-wave rectifier, we shall consider it in conjunction with a peak rectifier circuit. Subsequently, we shall combine this full-wave rectifier circuit with a zener diode voltage regulator circuit to form a complete power supply circuit.
3.4.1 Half-Wave Rectifier
A half-wave rectifier circuit is shown in Fig. 3.20. It consists of a transformer with a 14:1 turns ratio, a single diode D1 of the commercial type 1N4148, and a load resistance Rload of 1 k-ohm. The source resistance of 0.5 ohm of the AC line is also included in this circuit. The purpose of the transformer is to step down the main household AC power supply voltage of 120 V-rms to a 12 V-peak level. Spice does not make provision for an ideal transformer, probably for a good reason; one does not exist in practice. Instead, Spice allows coupled inductors to be described having a coefficient of coupling k less than one. Two inductors, say for example, LP and LS, which share a common magnetic path and have a coefficient of coupling k very close to unity, say 0.999, would be a reasonably good model of many practical transformers. The turns ratio NP/NS of such a transformer is given by the square-root of the ratio of the primary to secondary inductance, i.e., NP/NS = ÖLP/ÖLS.
To describe such a transformer to Spice, three element statements are required: One statement for each inductor, and a statement that describes the coefficient of coupling between the two inductors. Inductor coupling is described to Spice using a new statement that begins with the letter K. If more than two inductors share a common magnetic path, then a unique name is attached to K to uniquely identify each coefficient of coupling. This is then followed by the names of the two inductors that are magnetically coupled together. These names must correspond with the names of two inductors described in the present Spice deck. Subsequently, the final field of this statement describes the coefficient of coupling k, which can take on a value between 0 and 1. Since Spice does not accept a value of k equal to unity, we shall always in this book use k=0.999. The transformer ``dot'' convention is adhered to in Spice. Observe that the ``dot'' of each transformer is located at the positive node (n+) of each inductor. Extension to three or more coupled inductors should be self-evident. For a transformer, Fig.3.21 illustrates the three Spice statements necessary to describe it to Spice.
|
Fig. 3.22: Preparing the half-wave rectifier circuit shown in Fig. 3.20 for Spice analysis: A large-valued isolation resistor (100 MW) is placed between the secondary side of the transformer and ground. This provides a DC path between the secondary side of the transformer and the common reference node (0). Also added is a zero-valued voltage source in series with the rectifier diode. This will allow indirect access to the diode current.
|
Half-Wave Rectifier Circuit
** Circuit Description **
* ac line voltage Vac 5 0 sin (0 169V 60Hz) Rs 5 1 0.5 * transformer section Lp 1 0 10mH Ls 2 4 51uH Kxfrmr Lp Ls 0.999 * isolation resistor (allows secondary side to pseudo-float) Risolation 4 0 100Meg * diode current monitor VD1 2 6 0 * rectifier circuit D1 6 3 D1N4148 Rload 3 4 1kOhm * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** .TRAN 0.5ms 100ms 0ms 0.5ms ** Output Requests ** .plot TRAN V(3,4) V(2,4) V(1) .plot TRAN V(6,3) .plot TRAN I(VD1) .probe .end
Fig. 3.23: The Spice input file for calculating the transient behavior of the half-wave rectifier circuit shown in Fig. 3.20.
|
Returning to the half-wave rectifier circuit of Fig. 3.20, we can create a Spice description of this circuit. We shall assume that the inductance of the primary side of the transformer is 10 mH, and the inductance of secondary side is 51 mH. This will provide an effective transformer turns ratio of 14:1. Continuing, the alert student will quickly realize that the circuit on the secondary side of the transformer has no DC path to ground and will therefore be rejected by Spice. To circumvent this situation, we simply add a large resistor between ground and one point on the secondary side. The value of this resistor should be chosen such that it does not significantly interfere with the operation of the circuit. Fig. 3.22 illustrates the addition of a 100 M-ohm between ground and node 4 of the rectifier. Also shown in this figure is a zero-valued voltage source placed in series with the rectifier diode D1. This will enable us to monitor the current flowing through the diode. The resulting Spice deck for this modified circuit is seen listed in Fig. 3.23.
A transient analysis is requested to compute the voltage appearing across the load resistance, the voltage appearing across the primary- and secondary-side of the transformer, and finally, the AC line voltage. The Spice model of the commercial diode, 1N4148, was obtained from a library of Spice models for various electronic components included in PSpice[3].
|
Fig. 3.24: Various voltage waveforms associated with the half-wave rectifier circuit shown in Fig. 3.22. The top graph displays both the AC line voltage and the voltage appearing across the primary side of the transformer. The bottom graph displays the voltage appearing across the load resistor and the voltage appearing across the secondary side of the transformer.
|
Fig. 3.25: Zooming-in on a half cycle of the voltage waveform appearing across the load resistor and comparing it to the voltage developed across the secondary-side of the transformer.
|
The results of the Spice analysis are shown in Fig. 3.24. The top graph displays the voltage waveform of the AC line voltage (Vac) and the voltage appearing across the primary side of the transformer. Here we see that the voltage across the transformer experiences a short transient effect, quickly settling into its steady state with the transformer voltage slightly lagging behind the line voltage. The bottom graph displays the rectified voltage appearing across the load resistance and the voltage appearing across the secondary side of the transformer. A blown-up view of a half period of the rectified output voltage and the transformer secondary-side voltage is shown in Fig. 3.25.
An important consideration in the design of rectifier circuits is the diode current-handling capability, determined by the largest current that it has to conduct, and the peak inverse voltage (PIV) that the diode must be able to withstand without breakdown. In Fig. 3.26 we display both the voltage across the diode and the current that it conducts. We see that the PIV of this particular rectifier circuit is 12 V. Because the diode has not broken down, we can assume that the breakdown voltage of the 1N4148 commercial diode is larger than 12 V. In fact, data sheets of the 1N4148 diode indicate that its breakdown voltage is in the vicinity of 100 V. The maximum current that the diode has to conduct is seen to be about 11 mA. Using the cursor facility of Probe, we find that it is 11.1 mA. The data sheets of the 1N4148 indicate that this diode can handle a peak current of no more than 100 mA, thus our rectifier design is well within the limits of the 1N4148.

Fig. 3.26: The voltage and current waveform associated with diode D1. The peak inverse voltage (PIV) is seen to be 12 V and the maximum diode current is 11.1 mA.
3.4.2 Full-Wave Peak Rectifier
Fig. 3.27(a) displays a circuit for a full-wave peak rectifier. It consists of a full-wave rectifier - diodes D1 and D2 and a center-tapped transformer - and a filter capacitor C to smooth the voltage that appears across the load resistor R. Also shown is the resistance of the input voltage source of 0.5 ohm. The transformer is center tapped with each coil on the secondary side having a turns ratio of 14:1 with respect to the primary coil. In Fig. 3.27(b) we display the circuit that we shall actually describe to Spice for analysis. An isolation resistance RIsolation has been added to the circuit on the secondary side of the transformer in order to provide a DC path to ground. Also added are two zero-valued voltage sources, one in series with each diode. This will enable us to view the current that flows through each diode.
|
(a)
(b)
Fig. 3.27: (a) A full-wave peak rectifier circuit. (b) Actual circuit set-up simulated by Spice.
|
Full-Wave Peak Rectifier Circuit
** Circuit Description **
* ac line voltage Vac 1 0 sin(0 169V 60Hz) Rs 1 2 0.5 * transformer section with center-tap Lp 2 0 10mH Ls1 3 4 51uH Ls2 4 5 51uH K12 Lp Ls1 0.999 K13 Lp Ls2 0.999 K23 Ls1 Ls2 0.999 * isolation resistor Risolation 4 0 100Meg * monitor diode current VD1 3 7 0 VD2 5 8 0 * full-wave peak rectifier circuit D1 7 6 D1N4148 D2 8 6 D1N4148 C 6 4 50u R 6 4 1k * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** .TRAN 0.1ms 100ms 0ms 0.1ms ** Output Requests ** .plot TRAN V(6,4) V(3,4) .plot TRAN I(VD1) I(VD2) .probe .end
Fig. 3.28: The Spice input file for calculating the transient response of a full-wave peak rectifier circuit.
|
In the following we shall analyze the rectifier circuit of Fig. 3.27 with Spice assuming that the peak rectifier has a load resistance of 1 kW and a smoothing capacitor of 50 uF. The two rectifier diodes will be assumed to be modeled after the commercial 1N4148. The Spice deck describing this circuit can be seen listed in Fig. 3.28. The center-tapped transformer is described by three inductor statements and three corresponding coupling statements specifying the coefficients of coupling:
|
* transformer section with center-tap Lp 2 0 10mH Ls1 3 4 51uH Ls2 4 5 51uH K12 Lp Ls1 0.999 K13 Lp Ls2 0.999 K23 Ls1 Ls2 0.999 |
To obtain a transformer with a primary to secondary turns ratio of 14:1 for each coil on the secondary side, we have assumed that each coil of the secondary side has an inductance of 51 uH. This, then, implies that the inductance of the primary must be 10 mH according to the relationship: NP/NS = ÖLP/ÖLS. Further, we have also assumed a rather ideal coefficient of coupling between each coil at a value near unity (0.999).
As our first analysis, we shall plot the voltage waveform that appears across the load resistor and the voltage waveform that appears across one coil on the secondary side of the transformer. This analysis will be performed over six periods of the input line voltage. Subsequently, we shall investigate the current that flows through each diode of the rectifier.

Fig. 3.29: Voltage waveforms associated with the peak-rectifier circuit shown in Fig. 3.27. One waveform is the voltage that appears across the load resistance R and the other waveform is the voltage that appears across LS1 on the secondary side of the transformer.
Fig. 3.29 displays the results of this analysis. As is evident, the voltage appearing across the load resistor initially ramps up from 0 V to a steady-state value that ripples somewhere between 10 and 11 V. Using the cursor facility of Probe, we are able to determine more precisely the minimum and maximum values of this output voltage waveform to be 9.53 and 10.8 V, respectively. Thus, the average voltage appearing across the load resistor is 10.17 V having a peak-to-peak ripple voltage of 1.27 V. Also shown in the graph of Fig. 3.29 is the voltage waveform appearing across the secondary-side coil LS1 of the transformer (see Fig. 3.27). Here we see that it settles into a sinusoidal with a peak value of 12 V. Thus, confirming that the transformer circuit is operating correctly and converting the AC line voltage of 120 V-rms to a 12 V-peak level.
According to a hand analysis, together with the assumption that the forward voltage drop across each diode is 0.8 V, the expected ripple associated with this circuit using the equation Vr = VP/(2 f C R) developed by Sedra and Smith, 3rd Edition, in Section 3.6 of their text is 1.86 V. This appears to be slightly larger than that observed from the above simulations. As we shall soon discover, the reason for the discrepancy is largely due to the large series resistance rS of 16 ohm associated with each diode (see the diode model for the 1N4148).
|
Fig. 3.30: The instantaneous current flowing through each diode of the rectifier.
|
Fig. 3.31: A close-up view of a single current pulse in steady state flowing through diode D2. |

Fig. 3.32: A close-up view of a single current pulse in steady state flowing through diode D2 when the bulk diode resistance rS is set to zero.
It is interesting to point out that the average load voltage (VL= VP - Vr/2) agrees quite closely with the value obtained from the above simulation at 10.26 V.
To further investigate the behavior of the full-wave peak rectifier circuit shown in Fig. 3.27, we have plotted the waveforms of the current that flows through each diode in Fig. 3.30. The top graph displays the current that flows through diode D1 and the graph below it displays the current waveform associated with diode D2. As is evident from the top graph, diode D1 conducts a rather large initial current pulse having a peak value of about 165 mA and seems to have reached steady-state behavior by the fourth current pulse. The current waveform associated with diode D2 does not reveal such a dramatic transient, instead it appears to have reached steady state by the third current pulse.
To see more closely a single steady-state pulse of the current that flows through diode D2, we expanded the horizontal scale of the bottom graph shown in Fig. 3.30 between 93 and 97 ms and plotted an expanded view of the current waveform shown there in Fig. 3.31. Here we find that the current pulse has a peak value of 57.7 mA and extends between 93.95 ms and 96.37 ms for a conduction period of 2.42 ms. We also notice that the shape of this current pulse is rather gaussian, unlike the right-angled triangular current pulse that results when the diode is assumed ideal.
According to the simple theory developed for full-wave rectifier circuits in Section 3.6 of Sedra and Smith, the expected conduction period Dt of each diode is given by
(3.9)

and the peak diode current iD,MAX (in steady-state) is given by
(3.10)

Substituting the appropriate numerical values, we estimate the conduction period of either diode in steady state to be 1.53 ms. Similarly, the peak diode current is expected to be 122.1 mA. Comparing these two results with those found through simulation (2.42 ms and 57.7 mA), we find that they differ significantly.
On investigation we discovered that the major reason for the discrepancies between theory and the Spice simulation is the presence of the nonzero bulk diode resistance rS. In the mathematical development of the formulae that describe the full-wave rectifier circuit, the series resistance associated with a practical diode was not accounted for (mainly to keep the mathematical description simple). If we repeat the above simulation with the rS term in the model statement set to zero we find that our simulation results correlate much more closely with those predicted by the above equations.
To illustrate this, we re-simulated the full-wave peak rectifier circuit shown in Fig. 3.27(b) with the following diode model for the 1N4148:
.model D1N4148 D (Is=0.1pA Rs=0 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
Here the Spice model parameter Rs was re-assigned a value of 0. On completion of the Spice job, we plotted the voltage across the load resistor and found a waveform that is similar to that seen previously in Fig. 3.29 and is therefore not shown here. The output voltage had an average value of 10.57 V with a peak-to-peak voltage ripple of 1.46 V.

‡ The numerical integration facility of Probe was used to compute the area under a single current pulse. This value was then divided by the conduction period Dt to obtain the average current.
Table 3.3: Various parameters of the full-wave peak rectifier circuit shown in Fig. 3.27 as computed by hand and the two Spice analyses. Here f represents the frequency of the input AC line voltage applied to the primary side of the transformer.
The steady-state current pulse associated with either diode D1 or D2 is quite different from that seen previously. As an example, we display in Fig. 3.32 a single current pulse in steady state flowing through diode D2. Here the shape of the current pulse is very much a right-angle triangle having a peak value of 115.2 mA and a conduction period of 1.60 ms. When these results are compared to those results predicted by Eqns. (3.9) and (3.10), (i.e., 122.1 mA and 1.53 ms), we see that we are in much better agreement.
To conclude this section, we present in Table 3.3 a comparison of various parameters of the full-wave peak rectifier circuit found from the above two Spice analysis with corresponding parameter values computed using the formulas derived in Section 3.6 of Sedra and Smith. These formulas are also provided in this table for easy reference. Included in this table is the average current that flows through each diode while it is forward conducting. Spice provides no direct way of accessing this current value from the simulated results. Instead, the area under a single current pulse was computed by using the numerical integration facility of Probe, then it was divided by the time that the diode is conducting current (i.e., conduction period) to obtain the average current flowing through the diode.
|
Fig. 3.33: A 5 V regulated power supply.
|
A Regulated Power Supply
* zener diode subcircuit .subckt zener_diode 1 2 * connections: | | * anode | * cathode Dforward 1 2 1mA_diode Dreverse 2 4 ideal_diode Vz0 4 3 DC 4.9V Rz 1 3 10 * diode model statements .model 1mA_diode D (Is=100pA n=1.679 ) .model ideal_diode D (Is=100pA n=0.01 ) .ends zener_diode
** Main Circuit ** * ac line voltage Vac 1 0 sin(0 169V 60Hz) Rs 1 2 0.5 * transformer section with center-tap Lp 2 0 10mH Ls1 3 4 51uH Ls2 4 5 51uH K12 Lp Ls1 0.999 K13 Lp Ls2 0.999 K23 Ls1 Ls2 0.999 * isolation resistor Risolation 4 0 100Meg * full-wave peak rectifier circuit D1 3 6 D1N4148 D2 5 6 D1N4148 C 6 4 583uF R 6 7 160 * zener diode XZ1 4 7 zener_diode * load Rload 7 4 500 * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** .OPTIONS ITL5=0 .TRAN 0.5ms 200ms 0ms 0.5ms UIC ** Output Requests ** .plot TRAN V(7,4) V(6,4) .probe .end
Fig. 3.34: The Spice input file for calculating the time-varying output voltage of the 5 V regulated power supply shown in Fig. 3.33. Changing the ITL5 internal parameter of Spice through an .OPTIONS command resets the transient analysis total iteration limit. Setting ITL5=0 increases this limit to infinity.
|
3.4.3 A Voltage Regulated Power Supply
To complete this section on rectifier circuits we shall analyze a commonly used power supply configuration with Spice. Consider the circuit shown in Fig. 3.33. It can be thought of as consisting of three parts: a full-wave peak rectifier, a zener diode voltage regulator and the load. The peak rectifier circuit acts to supply a relatively stable DC voltage to the zener regulator which, in turn, reduces any voltage fluctuation (ripple) that appears on it. In addition, the voltage regulator acts to maintain a constant voltage across the load for a wide range of load currents. Resistor RIsolation is used for Spice simulation purposes and plays no role in the circuit function.
Let us consider using the circuit configuration shown in Fig. 3.33 to design a 5 V power supply for an application that requires a maximum load current of 20 mA. The 120 V-rms AC household voltage is stepped down to a 12 V-peak level using a center-tapped transformer with each coil on the secondary side having a turns ratio of 14:1 with respect to the primary coil. Further, we have at our disposal a zener diode that has VZ=5.1 V at a current of 20 mA and has a dynamic resistance rz=10 W. We also know that the minimum zener diode current must be limited to 5 mA if we are to maintain the diode in its breakdown region. Assuming that the input voltage to the voltage regulator circuit ranges between 9 and 12 V, we choose the current limiting resistor R from the expression (derived in Section 3.5 of Sedra and Smith):
(3.11)

Thus, we obtain R=160 W. As a point of reference, under worst-case conditions, the expected minimum output voltage is about 4.95 V as calculated from the expression, VOmin = VZ0 + rz IZmin.
The size of the smoothing capacitor is to be determined so that the voltage applied to the regulator circuit does not go below 9 V. Assuming that the peak voltage appearing across the secondary-side of the center-tapped transformer is 12 V, then the worst-case ripple voltage must be limited to no more than 3 V. We shall limit the ripple voltage to a more conservative 1 V level in case the peak voltage level changes. We can then estimate the size of the capacitor we require by using the formula for the ripple voltage provided in Table 3.3 for a full-wave peak rectifier. Substituting R=160 ohm, Vr=1 V, VP=11.2 V (accounting for a 0.8 V diode drop) and f=60 Hz, we get C=583 uF. This capacitance may seem large but is typical of the size of capacitor used in power supplies.
To investigate whether our design meets the required specifications, we shall simulate the power supply circuit shown in Fig. 3.33 with an initial load resistance of 500 W. This load should draw an average current of no more than 10 mA - well within the maximum load current condition. The Spice deck for this circuit is seen listed in Fig. 3.34. The transformer is represented by a primary inductance of 10 mH, and the two coils on the secondary side are each assigned a value of 51 uH. The two rectifier diodes are assumed to be modeled after the commercial diode type 1N4148.
The first analysis that we shall perform with Spice is to determine whether the output voltage is nominally 5 V. This can be determined by observing the voltage across the load resistance. Due to the presence of the large smoothing capacitor C, a long charge-up time will be necessary before the power supply circuit reaches steady-state. Therefore, a request for a long transient analysis is necessary to observe steady-state behavior. Here we have selected that the transient be computed over a 200 ms interval. Moreover, because of this long time interval, many iterations of the transient analysis algorithm will be performed by Spice. If the number of iterations performed by Spice exceeds 5000, Spice will stop the analysis. To allow more than 5000 iteration, we can reset this limit by reassigning a new value to the Spice internal parameter ITL5. This is accomplished by including an .OPTIONS command line in the Spice deck with the new value of ITL5, i.e.,
.OPTIONS ITL5=0.
Note that Spice recognizes that ITL5=0 really means ITL5=¥, or in other words, ignore this test and allow as many iterations as is necessary. In almost all cases, the number of iterations required to complete a given analysis is not known a priori, thus it is simplest to just use ITL5=0.
On completion of the Spice analysis, the voltage waveform that appears across the 500 ohm load resistor is shown in Fig. 3.35. Also shown is the voltage that appears across the smoothing capacitor C. As we can see, the voltage across the capacitor has an average value of about 9.5 V and a peak-to-peak ripple of 0.25 V. In contrast, the voltage across the load resistor is quite close to 5 V. Using the cursor facility of Probe, we find that the load voltage ripples slightly, between 5.065 and 5.080 V, a ripple voltage of only 15 mV. We therefore see that the above power-supply design is operating quite close to the nominal design, providing an output voltage of 5 V at a load current of about 10 mA.
|
Fig. 3.35: The voltage across the smoothing capacitor C of the peak rectifier, and the output voltage across the 500 W load resistance.
|
Fig. 3.36: The output voltage waveform from the 5 V power supply for load resistances of 150, 200, 250 and 500 W. The voltage regulation is lost at a load resistance of 150 W.
|
To see the effect of larger current demands on the power supply, consider reducing the load resistance. In order to compare the effect of different loads, we shall re-simulate the circuit with load resistances of: 150, 200 and 250 ohm. Assuming that these load resistances do not significantly affect the output voltage, they would correspond to a load current of: 33.3 mA, 25 mA and 20 mA, respectively. Using the same Spice deck as shown in Fig. 3.34 with only the value of the load resistance altered, we concatenated three similar files, together with the original one having a load of 500 ohm, into one file for processing. As a result of the analysis, we display a view of the output voltage over the time interval 160 to 200 ms in Fig. 3.36. As is clearly evident, for load resistances greater than and including 200 ohm, the output voltage is maintained very near the 5 V level with very little ripple visible. However, for a load resistance of 150 ohm, we see that the output voltage level has dropped down to an average value of about 4.5 V. Also, we see that the ripple voltage associated with this signal has increased significantly. This suggests that the output voltage is no longer being regulated. This is because the zener diode has been starved of its current and has turned off.
We conclude that the power supply circuit shown in Fig. 3.33 will provide a constant 5 V output level for load currents at least as large as 25 mA.
|
Fig. 3.37: A back-to-back diode limiter circuit.
|
A Diode Limiter Circuit
** Circuit Description **
Vi 1 0 DC 0V R 1 2 1k D1 2 0 D1N4148 D2 0 2 D1N4148 * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** * sweep the input voltage level from -5 V to +5 V in 100 mV increments .DC Vi -5V 5V 100mV ** Output Requests ** .PLOT DC V(2) .probe .end
Fig. 3.38: The Spice input file for calculating the DC transfer characteristic of the back-to-back diode limiter circuit of Fig. 3.37.
|
3.5 Limiting and Clamping Circuits
In the following we shall simulate the circuit operation of several commonly used diode circuits. This will include the analysis of a back-to-back diode limiter circuit, a DC restorer circuit and a voltage doubler circuit.
A Diode Limiter Circuit
In Fig. 3.37 we present a simple back-to-back diode limiter circuit constructed with two diodes of the 1N4148 type. Using Spice, we would like to observe the transfer characteristic of such a circuit. The Spice deck for this circuit is shown in Fig. 3.38. Here we are sweeping the input DC source vI between -1 and +1 V.
The results of this analysis are shown in Fig. 3.39. Here we see that the transfer characteristic exhibits rather soft limiting with the linear region ranging between -0.5 V and +0.5 V. The slope in the linear region is found to be unity.

Fig. 3.39: DC transfer characteristic of the back-to-back diode limiter shown in Fig. 3.37.
A DC Restorer Circuit
In Fig. 3.40 we present a DC restorer or a clamped capacitor circuit. Using Spice, we would like to observe the transient behavior of this circuit with a square-wave input having a 10 V peak-to-peak amplitude, a +2 V DC offset, and a 1 kHz frequency. The diode will be assumed to be of the 1N4148 type, and the capacitor has a 1 uF value. The Spice deck for this particular example is shown in Fig. 3.41. The square-wave input is described by the following source PULSE statement:
Vi 1 0 PULSE ( -3 7 0s 10us 10us 0.490ms 1ms ).
It goes between -3 and 7 V with 0 s delay, a rise and a fall time of 10 us and has a period of 1 ms.
The results of the Spice transient analysis are shown in Fig. 3.42. The top graph displays the input 10 V square-wave signal and the bottom graph shows the corresponding signal that appears at the output. We see that it is also a 10 V square-wave, but its DC level has now changed to a 5 V level (one-half the peak-to-peak value).
|
Fig. 3.40: A DC restorer circuit. |
A DC Restorer Circuit
** Circuit Description ** Vi 1 0 PULSE ( -3 7 0s 10us 10us 0.490ms 1ms ) C1 1 2 1u D1 0 2 D1N4148 * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** .TRAN 100u 10m 0m 100u ** Output Requests ** .PLOT TRAN V(1) V(2) .probe .end
Fig. 3.41: The Spice input file for calculating the time-varying output voltage from the DC restorer circuit shown in Fig. 3.40.
|

Fig. 3.42: The input and output voltage waveforms of the associated with the DC restorer circuit of Fig. 3.40.
Voltage Doubler Circuit
In Fig. 3.43 we show a voltage doubler circuit. Using Spice, we would like to observe the transient behavior of this circuit for an input sine-wave signal having a 10 V amplitude and a 1 kHz frequency. The diodes will be assumed to be of the 1N4148 type, and the two capacitors are of the same value at 1 uF. The Spice deck for this particular example is shown in Fig. 3.44.
The results of the Spice transient analysis are shown in Fig. 3.45. The top graph displays the input 10 V-peak sinewave, the middle graph displays the voltage that appears across diode D1 and the bottom graph shows the voltage that appears at the output of the doubler circuit. Looking at the output voltage waveform in the bottom graph we see that it experiences a transient that lasts for about 7 ms and then settles to a constant level of -18.8 V. The magnitude of this signal is approximately twice the peak value of the input sine-wave signal. The voltage across diode D1 settles into a 10 V-peak sine-wave signal with a -10 V DC offset.
|
Fig. 3.43: A voltage doubler circuit.
|
A Voltage Doubler Circuit
** Circuit Description ** Vi 1 0 sin ( 0 10V 1kHz ) C1 1 2 1u C2 3 0 1u D1 2 0 D1N4148 D2 3 2 D1N4148 * diode model statement .model D1N4148 D (Is=0.1pA Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p)
** Analysis Requests ** .TRAN 100u 10m 0m 100u ** Output Requests ** .PLOT TRAN V(1) V(2) V(3) .probe .end
Fig. 3.44: The Spice input file for calculating the transient response of the voltage doubler circuit shown in Fig. 3.43.
|

Fig. 3.45: Various voltage waveforms of the voltage doubler circuit shown in Fig. 3.43. The top graph displays the input sine-wave voltage signal, the middle graph displays the voltage across diode D1, and the bottom graph displays voltage that appears at the output.
3.6 Spice Tips
· In some circuit situations, a DC path does not exist between a node in the circuit and the ground reference node 0. This causes a problem for Spice. The problem can be circumvented by placing a large resistor between this node and ground. The value of this resistor should be large enough so as not to interfere with the circuit operation.
· Spice can emulate the behavior of a laboratory curve-tracer through the application of the DC sweep command.
· The effect of temperature on a circuit can be investigated using Spice.
· An ideal diode can be very well approximated by setting the emission coefficient n of the diode model between 0.01 and 0.001.
· A zener diode cannot be properly represented by the diode model statement found in Spice. Instead, a zener diode is represented by a subcircuit consisting of several diodes, a voltage source and a resistor - See Fig. 3.13.
· An ideal transformer is not represented in Spice; instead it is closely approximated by two inductors with a coefficient of mutual coupling very close to one (i.e., k=0.999).
· Commercial vendors of electronic components are making available Spice models of their devices and circuits. This should greatly improve the range of circuits that can be simulated by Spice.
· Provided with the student version of PSpice is a series of device models for several commercial parts. These are found in a file named NOM.LIB located in the same directory that the PSpice program is located in.
· When performing long transient runs, to ensure that Spice does not stop after 5000 iterations of the transient analysis, the parameter ITL5 can reset this limit to some other value. Since, in most circuit simulations, one does not know {\it a priori} the number of iterations the transient analysis will require, it is best to set this limit to infinity. This is accomplished by setting ITL5=0.
3.7 Problems
3.1. Assuming that the diodes in the circuits of Fig. P3.1 are modeled with parameters: IS=10-14 and n=2. Determine, with the aid of Spice, values of the labeled voltages and currents. Repeat with diode parameters: IS=10-12 and n=1.
3.2. Consider the battery charger circuit shown in Fig. P3.2. If vS is a 60 Hz sinusoid with 24 V-peak amplitude, find the fraction of each cycle during which the diode conducts. Also find the peak value of the diode current and the maximum reverse-bias voltage that appears across the diode. Assume that the diode has Spice model parameters: IS=10-12 and n=1.6.
3.3. If the sinusoidal source of Problem 3.2 is replaced by a square wave of the same frequency and amplitude, for what fraction of the cycle does the diode conduct?

(a) (b)
Fig. P3.1


Fig. P3.2 Fig. P3.5
3.4. Repeat Problem 3.2 for a symmetrical triangular wave of 24 V amplitude.
3.5. Simulate the circuit shown in Fig. P3.5 with Spice and determine the DC transfer characteristic. Assume that each diode is of the 1N4148 type. See Fig. 3.23 for the Spice model parameters for this diode.
3.6. Use the Spice operating point command (.OP) to determine what the incremental resistance is for 10 diodes of the 1N4148 type connected in parallel and fed with a DC current source of 10 mA. See Section 3.6 for the model parameters of the 1N4148.

Fig. P3.7
3.7. For the circuit shown in Fig. P3.7 with Rs=1 k-ohm, C=1.0 uF, and I having several values of 1 mA, 0.1 mA, and 1 uA, verify that the signal component in the output voltage for each case is given by:

Using Spice, simulate the transient behavior of this circuit with an input 100 Hz sine-wave signal of 1 mV-peak amplitude. Assume that the diode has model parameters IS=10 fA and n=2.
3.8. A voltage regulator consisting of two diodes in series fed with a constant current source is used as a replacement for a single carbon-zinc (battery) cell of nominal voltage 1.5 V. The regulator load current varies from 2 to 7 mA. Compare this regulator circuit for three different current source levels of 5, 10 and 15 mA as the load current varies over its full range. What is the change in the output voltage for each case? Assume that the diodes have a 0.7 V drop at a 1 mA current and n=2.}
3.9. A zener shunt regulator of the type shown in Fig. 3.14 has been designed to provide a regulated voltage of about 10 V. The zener diode is of the type 1N4740 which is specified to have a 10 V drop at a test current of 25 mA. At this current its rz=7 ohm. The raw supply available has a nominal value of 20 V but can vary by as much as ±25%. The regulator is required to supply a load current of 0 to 20 mA. Assuming that the minimum zener current is to be 5 mA, the resistance R was determined to be 200 ohm. Using Spice, simulate the behavior of this circuit and:
(a) Find the load regulation. By what percentage does VO change from the no-load to full-load condition?
(b) Find the line regulation. What is the change in VO expressed as a percentage, corresponding to the ±25% change in VS.
(c) What is the maximum current that the zener diode has to conduct? What is maximum zener power dissipation?

Fig. P3.10
3.10. For the half-wave rectifier circuit of Fig. P3.10. Let vS be a sinusoid with a 10 V-peak amplitude and let R=1 kW. Assume that diode has diode parameters IS=100 pA and n=1.679. Using Spice:
(a) Calculate and plot the transfer characteristic.
(b) Calculate and plot the output voltage waveform assuming that the input signal frequency is 1 kHz. Estimate the average value of this output signal.
(c) Determine the peak current in the diode.
(d) Determine the PIV of the diode.
3.11. Consider a half-wave rectifier circuit with a triangular input of 20 V peak-to-peak amplitude and zero average. The resistance in series with the diode is 1 k-ohm. Assume that the diode has model parameters IS=100 pA and n=1.679. Calculate the output voltage and estimate the average value of this output signal.

Fig. P3.12
3.12. It is required to design a full-wave rectifier circuit using the circuit of Fig. P3.12 to provide an average output voltage of:
(a) 10 V.
(b) 100 V.
In each case find the required turns ratio of the transformer assuming LP=10 mH and check your results using Spice. Assume that the diodes are of the 1N4148 type, the ac line voltage is 120 V-rms and has a source resistance of 0.5 ohm.

Fig. P3.13
3.13. The circuit in Fig. P3.13 implements a complementary-output rectifier. Simulate the behavior of this circuit using Spice and plot the voltage that appears across the two output terminals. Assume that the diodes have model parameters IS=100 fA and n=2. What is the PIV of each diode?
3.14. Design a half-wave peak rectifier circuit that provides an average DC output voltage of 15 V on which a maximum ±1 V ripple is allowed. The rectifier feeds a load of 150 ohm and the rectifier is fed from the line voltage (120 V-rms at 60 Hz) through a transformer. The diodes are assumed of the type 1N4148. Simulate the operation of your design using Spice and verify that it indeed satisfies the design requirements.

Fig. P3.15
3.15. Using Spice, plot the transfer characteristic vO versus vI for the four limiter circuits shown in Fig. P3.15. Assume that the diodes have model parameters IS=100 fA and n=1.6.

Fig. P3.16
3.16. Using Spice, plot the transfer characteristic vO versus vI of the circuit in Fig. P3.16 for -20 V £ vI £ +20 V. Assume that the diodes have model parameters IS=100 fA and n=1.6, and that the zener diode has a reverse-bias voltage drop of 8.2 V at a current of 10 mA and rz=20 ohm.
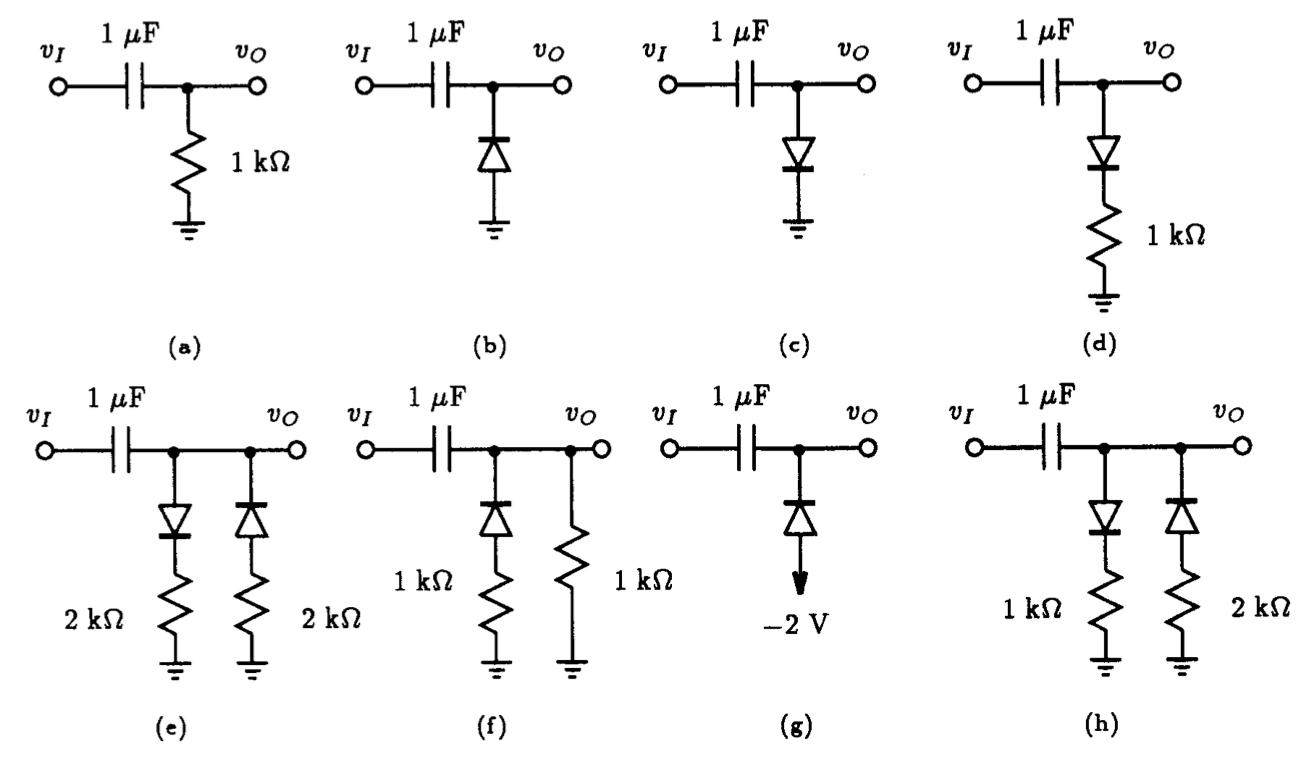
Fig. P3.17
3.17. For the circuits in Fig. P3.17, each utilizing diodes of the 1N4148 type, plot the output waveform of the circuit for a 10 V-peak amplitude input square-wave having a frequency of 1 kHz.